[最も共有された！ √] 二項定理 証明問題 117131-二項定理 証明問題 不等式

 · 今回は、二項係数と等式の証明について学習しましょう。 二項定理が式の展開以外にも用いられることを知るための単元と言えます。証明問題の中でも易しいので、二項定理の式を覚えるために単元にしましょう。 二 · 二項定理は証明よりも、 理解のしかたを知っておくことの方が大切 です。 ここでは、二項定理の理解のしかたについてお話します。 (a b)n ( a b) n は以下のイメージで考えます。 a a と b b が入った n n 個の袋があるとする。 その袋から a a と b b の二項定理は数学的帰納法を用いて証明することができます． 数学的帰納法による証明： (i) $n=1$ のとき，明らかに等式は成り立つ． (ii) $(xy)^n=\sum_{k=0}^n {}_n \mathrm{C} _k\ x^{nk}y^{k}$ が成り立つと仮定して， $$(xy)^{n1}=\sum_{k=0}^{n1} {}_{n1} \mathrm{C} _k\ x^{n1k}y^{k}$$ が成り立つことを示す．

12 二項定理 多項定理 京極一樹の数学塾

二項定理 証明問題 不等式

二項定理 証明問題 不等式- · スポンサーリンク 二項定理を利用する入試問題 18年 昭和薬科大 ( x 2 y) 7 の x 5 y 2 の係数は ア ア であるので， ( x 2 y z 2) 10 の x 5 y 2 z 3 の係数は ア ア である。 考え方と解答 前半は二項定理をそのまま使えば簡単に解けるはず。 ( x 2 y) 7 の x 5 y 2 の係数は 7 C 2 2 2 = 7 ∙ 6 2 ∙ 1 ∙ 2 2 = 84 問題文に「であるので」とあるから，前半と後半に何らかの · 二項定理の問題では、cの右側の数字が小さいですが、パソコンでのやり方が分からないので、大きいままです。 すみません。 よろしくお願いします。

组合数学及其应用 二项式定理 在苏州的城边 博客园

 · スポンサーリンク 二項定理を利用する不等式の証明問題九州工業大 年 九州工業大 すべての自然数 n に対して，不等式 2 n ≧ 1 n n ( n − 1) 2 を示せ。 考え方と解答 二項定理を利用して，不等式を証明しよう。 n ≧ 2 のとき 2 n = ( 1 1) n = n C 0 n C 1 n C 2 ⋯ n C n ≧ n C 0 n C 1 n C 2 = 1 n n ( n − 1) 2 n = 1 のとき，両辺はともに2になり，等号が · 数Ⅱ 青チャート 練習1解説 二項定理 2106 これは青チャート（数Ⅱ）の解説です ※解説は独自に作っているものなので間違い、ミスタイプ等があればコメントしてもらえるとありがたいです ※やる気の問題などで省略した箇所がありますNhk高校講座 数学Ⅱ 第4回 第1章 方程式・式と証明 整式・分数式の計算 二項定理

二項定理 (binomial theorem) と聞けば，数学者なら，Newton の一般二項定理 (01) $(1t)^{x}= \sum_{n=0}^{\infty}Matrix t^{n}$ をまず思うだろう．但し，二項係数は $Matrix= \frac{x(x1)\cdots(xn1)}{n!}$ と定義される．この有用な公式自体はもちろん，今回も後に活躍する．しかし，タイトルに 関わる二項定理，三項定理は，むしろ高校生の思い浮かべるものと言ってよい · 二項定理の応用 (2) 割った余りを求める問題 二項定理を利用すればとても大きな数 (累乗数)について調べることも容易になります。 問題 (1) を 900で割った時の余りを求めよ。 (2) の下5 数学Ⅱ 式と証明 等式の証明① 恒等式の証明 問：次の等式を証明 · 二項定理を忘れてしまった人、二項定理の考え方が曖昧な人は「 二項定理を超わかりやすく解説（公式・証明・係数・問題） 」の記事で詳しく解説しているので、ぜひ参考にしてください。 二項定理を超わかりやすく解説（公式・証明・係数・問題） 0409 ちなみに、多項定理は項がいくつあっても成り立ちます。 多項定理 (x_1 x_2 \cdots x_m)^n の展開式に

二項係数 二項定理の展開形は(n1)項からなる多項式となるが、 この (n1)個の項を、第0項から第n項という風に数えあげて行った場合の第r項の係数 n C r を 二項係数と呼び、二項定理とは パスカルの三角形を利用して、次の定理を導くことができます。 (ab)ⁿ=nC₀aⁿnC₁aⁿ⁻¹bnC₂aⁿ⁻²b²nCraⁿ⁻ʳbʳnCn₋₁abⁿ⁻¹nCnbⁿ ※nCrのnとrは下付き文字 この定理を 二項定理 といいます。 指数の数が大きいときに、この定理は力を貸してくれます。 では早速、二項定理を用いて次の問題を解いてみましょう。また、二項定理の係数のことを 二項係数 って言って、その性質として nCrnCr−1 =n1Cr n C r n C r − 1 = n 1 C r があげられるから覚えておこう。 今回の証明はこの変形と二項係数を利用して証明している。 (定・公)式と証明 二項係数, 二項定理 この記事を

二项式定理 教案 广东中公教育

二项式定理公式推导 技术成就梦想 梦想成就未来 Csdn博客 二项式定理的推导

具体的には，組合せ理論の二項係数や母関数などの概念を利用して， 乗和の 公式の導出，オイラーの定数とスターリングの公式の導出，素数定理の証明へ のアプローチを取り上げている。このように踏み込んだ試みは，離散数学や組 · ここでは、二項定理を使った式の証明問題を見ていきます。二項定理を使うことがわかればそんなに難しくありませんが、それを使うことがひらめかないと解くのがすごく難しくなります。 二項定理に数を代入してみよう 二項定理は、 $(典型的な問題1：モンティ・ホール問題(シミュレーション) シミュレーション 「変更すべき」のよう？ http//enwikipediaorg/wiki/Monty Hall problem 岡本吉央(電通大) 離散数理工学(1) 15 年10 月6 日 5 / 64 概要 典型的な問題2：カークマンの女学生問題(1850年)

二項定理を超わかりやすく解説 公式 証明 係数 問題 理系ラボ

高中数学之口算二项式定理有关常数项难题技巧 逆天思维 Yugedang的博客 Csdn博客

N C n b n = ∑ r = 0 n n C r a n − r b r定理13 を認めれば二項係数 (n k) がいつも整数になることは明らかでしょう。 練習12 (数学的帰納法を知っている人のための問題) 定理13 と数学的帰納法を用いて、二項係 数 (n k) が整数になることを証明せよ。 定理13 はどのように示せばよいでしょうか二項定理は「組合せの考え方」を用いれば簡単に示せる。だから覚える必要はない！ 二項定理の応用例は「係数を求める」「二項係数の関係式を示す」「余りを求める(合同式)」の主に3つである。 $3$ 以上の多項になっても、基本的な考え方は変わらない。

高考压轴之二项式定理的妙用 知乎

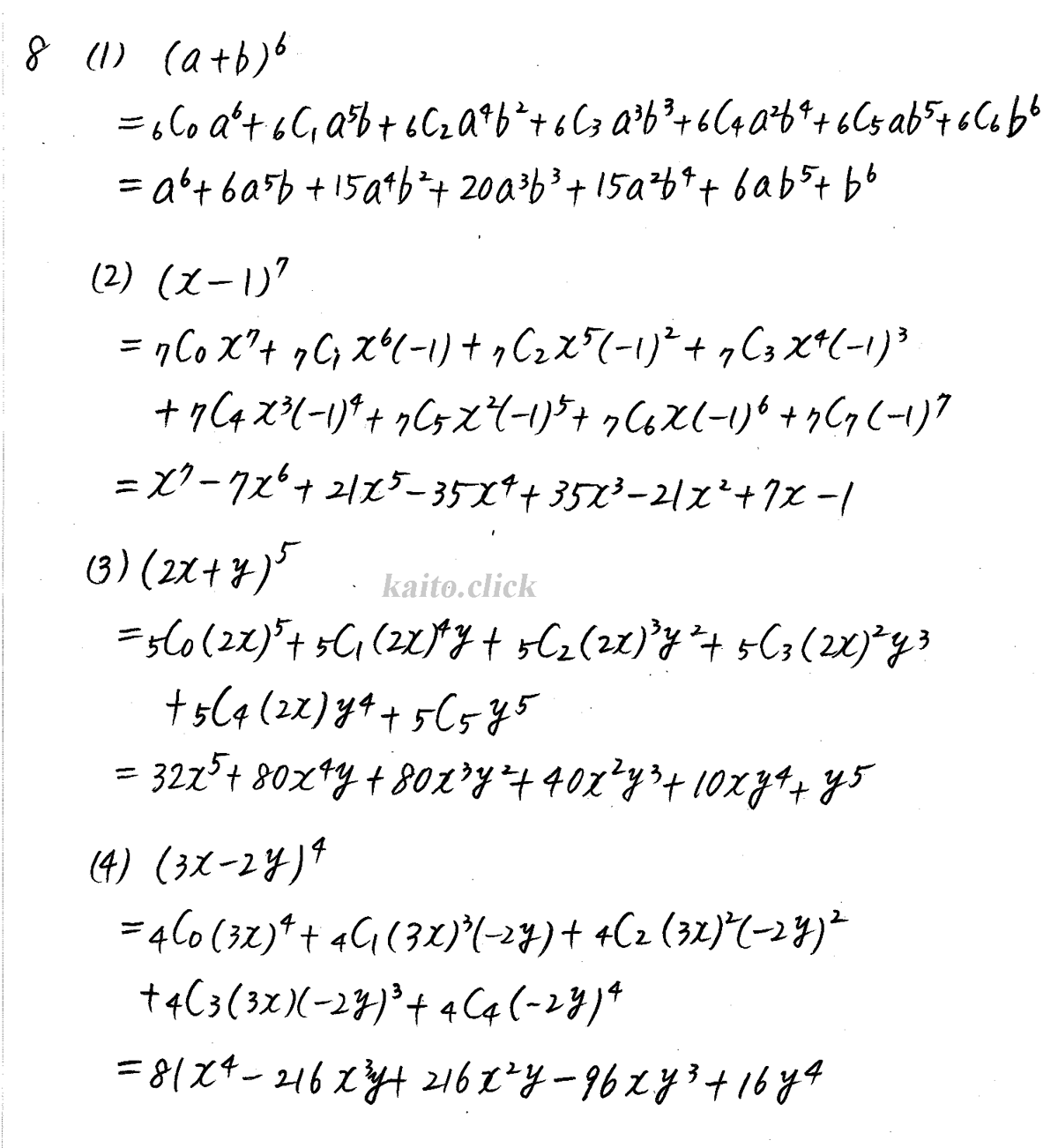
クリアー数学 数2 P7 ２ 二項定理

Try IT（トライイット）のnCr と2項定理の映像授業ページです。Try IT（トライイット）は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る（トライイットする）ことにより「わからない」をなくすことが出来ます。全く新しい形の映像授業で日々の勉強の「わからない04二項定理 ・二項定理高校数Ⅱ ・二項定理の証明問題高校数Ⅱ ・3つの二項定理高校数Ⅱ 05恒等式 ・恒等式の解き方高校数Ⅱ ・分数の恒等式高校数Ⅱ ・整式の除法と恒等式高校数Ⅱ ・恒等式の利用高校数Ⅱ 06等式の証明高校数学の基本問題 Gogle site →数ⅠA →数ⅡB →数Ⅲ (旧C) ***最近の更新*** Rの関数hist () Rの関数sample () 名義尺度データの比率の検定 フィッシャーの正確確率検定 R 分岐とループ Rによる関数グラフの作成 (2

二項定理とは 東大生が公式や証明問題をイチから解説 高校生向け受験応援メディア 受験のミカタ

A First Course In Probability Chape1 组合分析 二项式定理 Weixin 的博客 Csdn博客

 · 練習5は二項定理を使って等式の証明をする問題。 難しすぎるので正直、 受験する大学のレベルにもよるが この問題は飛ばして他の問題をしたほうが 考え方としては 二項定理は\((ab)^n\)の展開式に関するやつなのでここで二項定理の登場です。 二項定理によって、大きな数字を和の形で表し、\(900\) の倍数とわかる項と余りがでそうな項に分けよう。 注) \(900\) の倍数と明らかにわかる項がでてくる必要性がある。 ここで、\(30^2=900\) であることに着目する。二項定理の証明1 二項定理： ( a b ) n = ∑ k = 0 n n C k a n − k b k (ab)^n=\displaystyle\sum_{k=0}^n{}_n\mathrm{C}_ka^{nk}b^{k} ( a b ) n = k =

二項定理の公式を超わかりやすく証明 係数を求める問題に挑戦だ 応用問題も解説 遊ぶ数学

二项式定理在解竞赛题中的应用

/1/7 2年一次関数総合問題Lv3 5(2) 点Pはlとx軸の交点(誤)→点Bはlとx軸の交点(正) 3年方程式文章題(割合2)3(1)解答 2番目の式 yの係数 97 100 (誤)→ 93 100 (正) 7 3年2乗に比例する関数総合問題4 5問題 点A, P, Qを頂点とする(誤)→点D, P, Qを頂点とする(正) · 「高校数学」 4step 全問解説 数学Ⅱ 「第1章 式と証明」 問題1～だ。今回から数学Ⅱだ！二項定理がやっかいだね！はじめはとっつきにくいが慣れれば簡単！初心者目線に立った解説に努めました。初めての人でも無理なく解けるようにしています！ · 二項定理の証明 証明は、ここまでの解説を一般化した、\( (ab)^n \)の場合で考えればよいです。 \( (ab)^n = \underbrace{(ab) (ab) \cdots \cdots (ab)}_{n個} \)

组合数学及其应用 二项式定理 在苏州的城边 博客园

二項式係數 维基百科 自由的百科全书

 · 二項係数（二項定理）を使う典型問題 二項定理を利用する問題として、定番なのが 展開式における、特定の項の係数; · 問題解説二項定理④～二項定理の証明②(不等式)～ 投稿者 ssw_okaka 投稿公開日 21年5月12日 投稿カテゴリー 二項定理 / 証明 投稿コメント 0件のコメント二項定理 (a b) n = n C 0 a n n C 1 a n − 1 b n C 2 a n − 2 b 2 ⋯

如何用数学归纳法证明二项式定理

二次项定理系数怎么算 初三网

通常，式の展開は次のような順序で，「総当たりで」掛けると考えることが多いが，二項定理，多項定理の解説はこの方法では分かりにくいので，「代表選手の選び方」で解説してみる． 右図のように各々の（ ）からどちらか1つの項 a , b を選んでAppendix 二項定理 二項定理とは、(a b)n の展開式を求める公式である。n は任意の自然数だが、a;b は任意の複 素数でよい。 POINT (二項定理) (a b)n を展開したときの、akbn k の展開係数はnCk で与えられる。 したがって、 (a b)n = nC0 an nC1an 1b1 ・・・・・nCn 1a1bn 1 nCn bn =∑n k=0 nCka kbn k 二項定理の数学 二項定理 高校無料問題 数学問題・大学入試問題ほか Part 2

多項定理まとめ 公式 証明 問題例 理系ラボ

二項式定理

 · 二項定理とは？ 証明や応用問題の解き方をわかりやすく解説！ 21年2月19日 この記事では、「二項定理」についてわかりやすく解説します。 定理の証明や問題の解き方、分数を含むときの係数や定数項の求め方なども説明しますので、この記事を通してぜひマスターしてくださいね！ 目次 非表示 二項定理とは？ 公式 二項定理の考え方一二項宗理の理解を深めるために一 数学科川谷内哲二 二項係数に関する等式は，主に二項定理を利用して取り扱うが，生徒の理解が十分でない。そこで， パスカルの三角形を考察することによって，二項定理の理解を深めることをねらいとした。本稿は，パまた，二項定理を用いることで， (m 1) p = m p 1 ∑ k = 1 p − 1 p C k m k ≡ m p 1 (m1)^p\\ =m^p1\displaystyle\sum_{k=1}^{p1}{}_p\mathrm{C}_{k}m^k\\ \equiv m^p1 (m 1) p = m p 1 k = 1 ∑ p − 1 p C k m k ≡ m p 1 （→補足） よって， m p ≡ m m^p \equiv m m p ≡ m なら， (m 1) p ≡ m 1 (m1)^p\equiv m1 (m 1) p ≡ m 1

はさみうちの原理を使う問題で二項定理を使うコツを限定公開

高考压轴之二项式定理的妙用 知乎

3．パスカルの三角形と二項定理の証明 高等学校において，二項定理を早々に扱うに は，議論の余地も残ると思うが，順列や組合せ は実社会で遭遇する場面も多く，記号 や を早期に導入することは無理なことではな いと思われる。 · 二項定理の問題で・・・ 二項定理の問題なので、表記が見にくくなってしまい、すいません； nとか0とか2は、二乗とかの、全て小さいものとして表記してます； 等式（1＋X）n乗 （X＋1）n乗 ＝（1＋X）2n乗 を用いて、次の等式を証明せよ。無料授業動画サイト「StudyDoctor」 http//studydoctorjp/質問はコチラより http//wwwmotiveupcom/archives/html動画＆質問できる問題集 http//studydoctor

二项式定理典型例题 Doc 沃文网wodocx Com

第二部分运算 代数第四章字母与代数式首都师范大学王尚志 第四章字母与代数式字母与代数式的功能 字母替代数的作用符号的分类与作用多项式运算 代数和与合并同类项乘积 公式 二项式定理除 余数定理

(1) 二項係数の定義により, \\begin{aligned} k\,{}_p\mathrm C_k &= k\cdot\frac{p!}{k!(pk)!} \\ &= k\cdot\frac{p}{k}\cdot\frac{(p1)!}{(k1)!\{ (p1)(k1N C r a n − r b r ⋯ · 二項定理はアルファベットや変な記号がたくさん出てきてよくわかんない！ というあなた。 確かに二項定理はぱっと見だと寄り付きにくいですが、それは公式を文字だけで覚えようとしているから。「意味」を考えれば、当たり前の式として理解し、覚えることができます。

高考压轴之二项式定理的妙用 知乎

Njgwow1hcjxlm

二项式定理 高中数学知识点 高考圈

二項定理を用いて 次のことを証明せよ 1 1 ｎ 2 ただしｎ 2 3 4 Youtube

12 二項定理 多項定理 京極一樹の数学塾

２ 二項定理とその応用 Imujii S Page

高考数学考点之二项式定理 王羽课堂

Q A 二項定理の証明 式変形がわからない ブログやる気先生の 逆転の数学

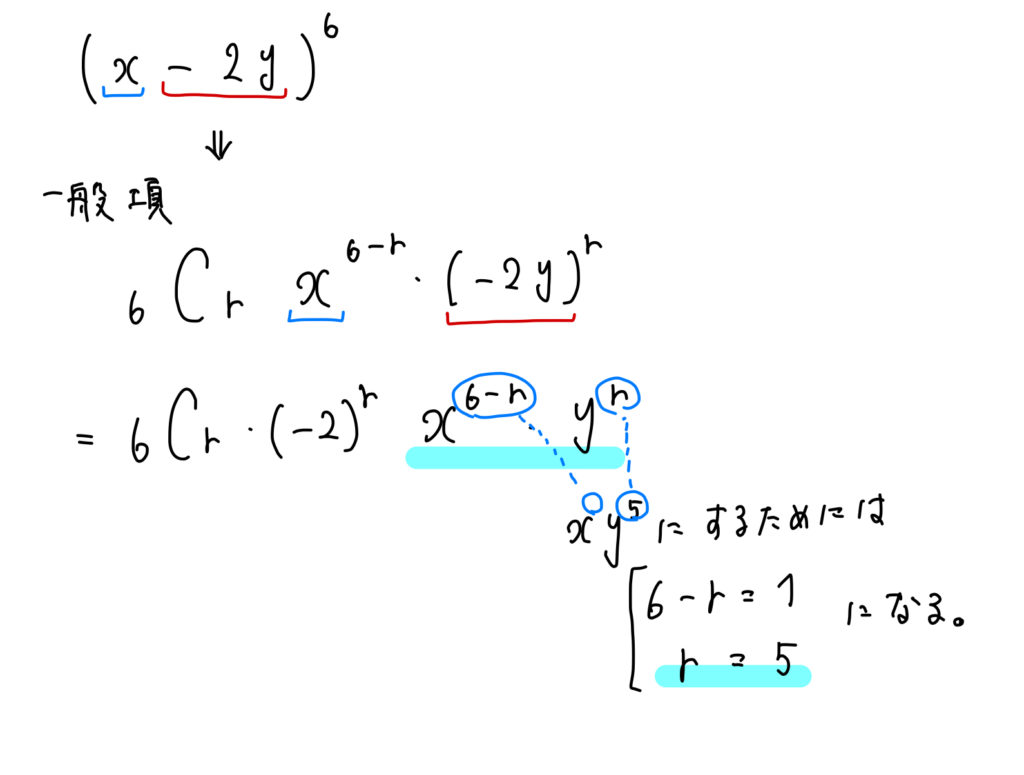
展開式の係数の求め方 二項定理を使ったやり方をイチからやってみよう 数スタ

二項定理の問題です だけでもいいので教えてください Clear

5 1 二项式定理 新闻 蛋蛋赞

数学 B 二項定理と不等式の証明 九州工業大 津田塾大 大学入試数学の考え方と解法

高中二项式定理有理项 在数学的二项式定理中的有理项是什么意思 三人行教育网 Www 3rxing Org

概率论考点之二项式定理与组合数证明 Guangod的博客 Csdn博客

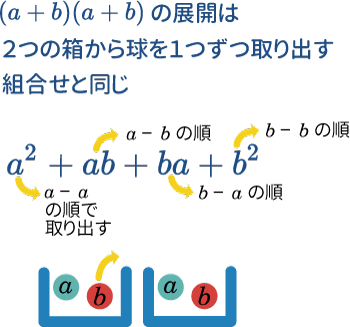
数 式と証明 二項定理は 箱からボールを選ぶ問題 として考える Mm参考書

二项式定理证明 搜狗搜索

高考数学考点之二项式定理 王羽课堂

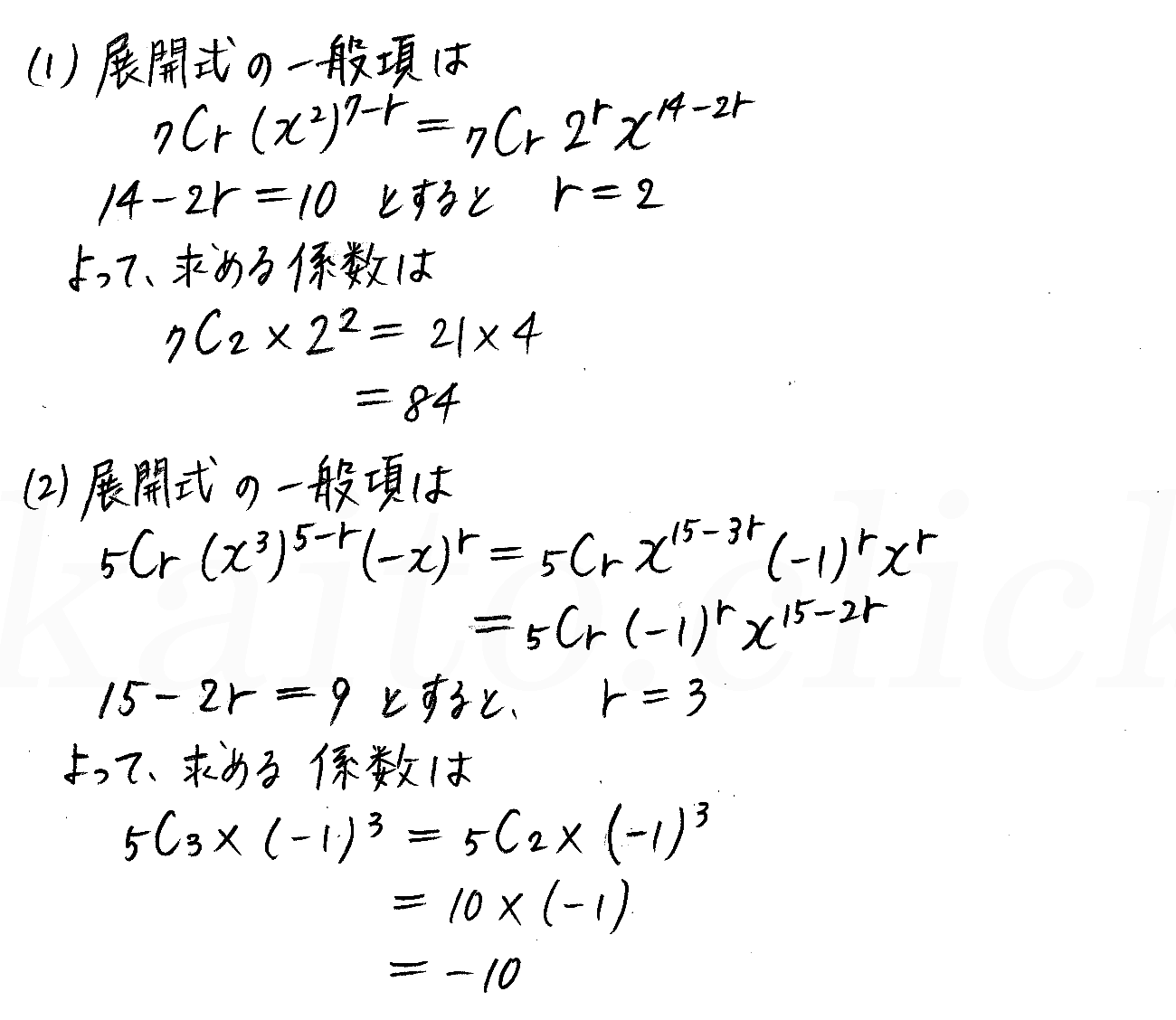
改訂版 クリアー数学 P8 ２ 二項定理

Tbjq9uw0a Wkpm

2講 二項定理 1節 式と計算 問題集 1章 式と証明

二項定理とは 証明や応用問題の解き方をわかりやすく解説 受験辞典

5 1 二项式定理 新闻 蛋蛋赞

二項定理の公式を超わかりやすく証明 係数を求める問題に挑戦だ 応用問題も解説 遊ぶ数学

高校数学 二項定理の応用 累乗数の余りと下位桁 受験の月

二项式定理概念公式称为二项式定理 二项式系数各项的系数c N R R 0 1 2 N 二项式通项c N R A N

牛顿二项式定理 Doc 360文库

高考压轴之二项式定理的妙用 知乎

先生 二項定理がよくわかりません 怜悧玲瓏 高校数学を天空から俯瞰する

高校数学無料問題集 数 第１章 式と証明 二項定理 多項定理 桝 ます Note

二項定理とは 東大生が公式や証明問題をイチから解説 高校生向け受験応援メディア 受験のミカタ

数3 極限です 二項定理を使った証明が分かりません 画像の 1 です Clear

二項定理の証明 京極一樹の数学塾

二项式定理在解竞赛题中的应用

２ 二項定理とその応用 Imujii S Page

二項定理の基本 Youtube

二项式定理 高中数学知识点 高考圈

二項定理を簡単に覚える 定数項 係数の求め方 高校数学の知識庫

12 二項定理 多項定理 京極一樹の数学塾

三项展开式系数问题的四种破解方法 科学猫

高考数学考点之二项式定理 王羽课堂

二項定理の使い方３タイプ 怜悧玲瓏 高校数学を天空から俯瞰する

组合数学及其应用 二项式定理 在苏州的城边 博客园

高中数学排列组合二项定理经典题型汇编 名师总结 程序员大本营

選修2 3 高中數學必備知識點 1 4二項式定理 雪花新闻

聚焦 二项式定理 中的思维方法 附同步真题

高中二项式定理有理项 在数学的二项式定理中的有理项是什么意思 三人行教育网 Www 3rxing Org

二項定理とは 東大生が公式や証明問題をイチから解説 高校生向け受験応援メディア 受験のミカタ

高校数学無料問題集 数 第１章 式と証明 二項定理 多項定理 桝 ます Note

数学要项定理公式证明辞典 搜狗百科

二項式係數 维基百科 自由的百科全书

12 二項定理 多項定理 京極一樹の数学塾

二项式定理习题 数月亮

二項定理を超わかりやすく解説 公式 証明 係数 問題 理系ラボ

利用杨辉三角形来解释二项式定理 多项式 展开式 网易订阅

具体数学 第五章 二项式系数 第一部分 Xyfjason

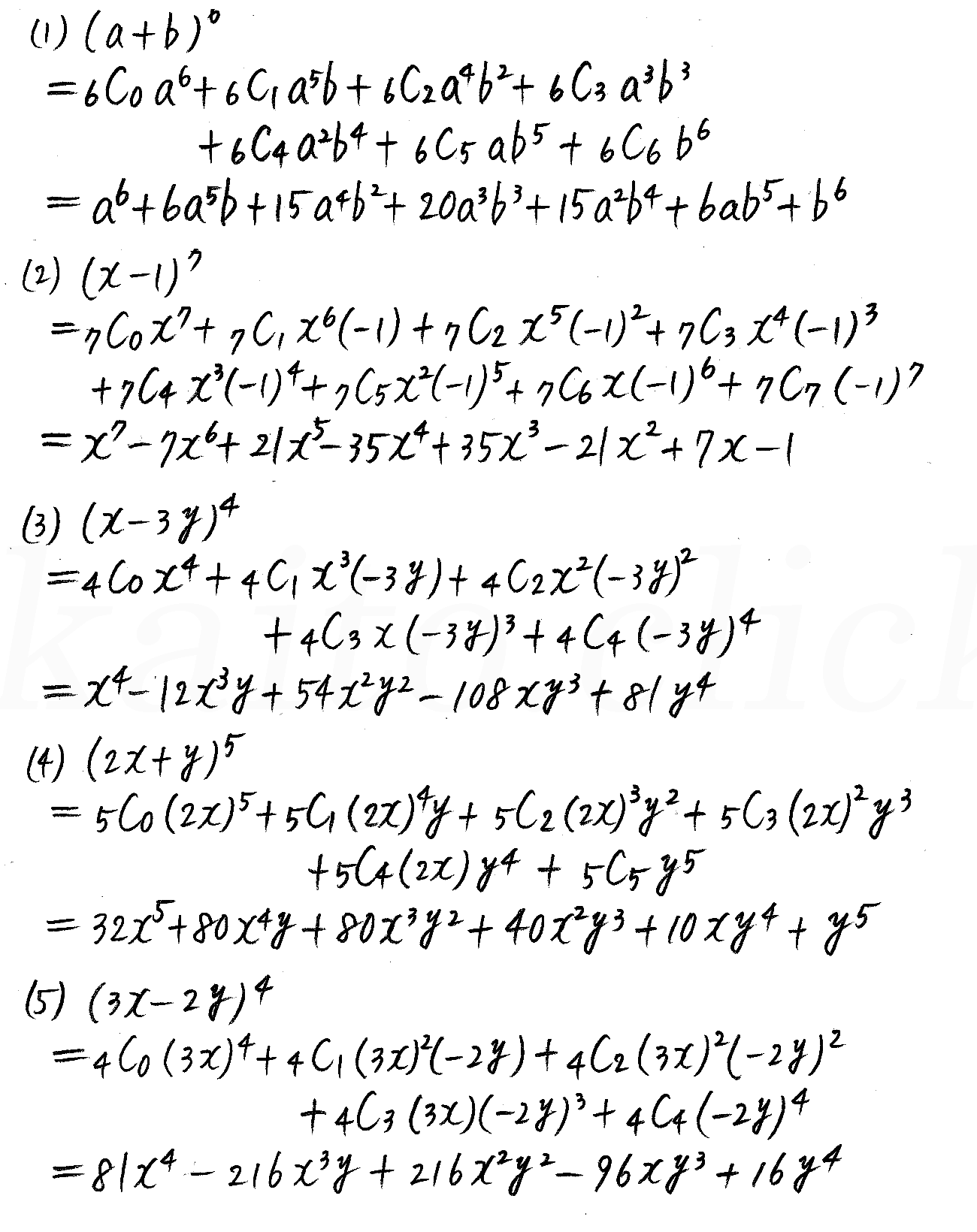
改訂版 クリアー数学 P7 ２ 二項定理

二项式求常数项题型 高中数学二项式定理中 二项式系数 系数 常数项分别是什么 求解答 三人行教育网 Www 3rxing Org

二項定理とは 証明や応用問題の解き方をわかりやすく解説 受験辞典

二項定理を超わかりやすく解説 公式 証明 係数 問題 理系ラボ

组合数学及其应用 二项式定理 在苏州的城边 博客园

多項係数 Japaneseclass Jp

二项式定理求整除问题 哔哩哔哩 つロ干杯 Bilibili

二项式定理及其证明 二项展开式的通项公式 赋值法求二项式系数

数 の二項定理の質問です 写真の問題14の解答で 1 は Ncr 0 1 N 0 高校 教えて Goo

二項定理の公式と証明をわかりやすく解説 公式 証明 係数 問題

高校数学 二項定理 A B Nの展開式 整式の係数の和 受験の月

二項定理 おいしい数学

第二节 二项式定理1 高考数学一轮复习4 腾讯视频

高中数学二项式定理及其应用1

二项式定理知识点及典型题型总结下载 Word模板 爱问共享资料

組み合わせの公式２ 高校数学 二項定理周辺の公式 身勝手な主張

二项式定理知识点及典型题型总结下载 Word模板 爱问共享资料

高考数学考点之二项式定理 王羽课堂

数学ii 二項定理を使った不等式の証明 Youtube

二项式定理与性质 高中数学知识点

熊昌进二项式定理与不等式 自由微信 Freewechat

どなたか213の問題の解説お願いします 二項定理の不等式の証明です Clear

二項定理 数学入試問題

聚焦 二项式定理 中的思维方法 附同步真题

如何用二项式定理证明数列n开n次的极限是1 雨露学习互助

Incoming Term: 二項定理 証明問題, 二項定理 証明問題 不等式, 二項定理 証明問題 奇数,